6 Simulating Data with R
這堂實習課將介紹 R 語言裡面一些非常實用的統計學函數,並會以實例示範如何透過這些函數去模擬 (simulate) 統計學裡常見的一些概念與現象。
6.1 分配 (Distribution)
R 內建許多統計分配的函數,例如
*unif(均勻分配, Uniform),*norm(常態分配, Normal),*binom(二項分配, Binomial),*pois(泊松分配, Poisson) 等-
每種分配都有一個「家族」的函數,用來做不同事情。例如,以常態分配為例 (詳見說明文件
?dnorm):-
dnorm(): 常態分配的機率密度 -
pnorm(): 常態分配的累積機率密度 -
rnorm(): 從常態分配抽取出來的樣本 (隨機數) -
qnorm(): 常態分配的 分位數 (quantile function)
-
接下來,我們會以常態分配作為例子示範。
6.1.1 dnorm()
我們可以使用 dnorm() 繪製常態分配 (鐘型曲線)。想法很簡單:
- 製造一個 (間距很小的) 數列
- 為每一個數列裡的值計算出相對應的機率密度
以平均 = 160、標準差 = 5 的常態分配 (台灣成人女性身高) 為例:
\[ Height \sim Normal(\mu = 160, \sigma = 5) \]
library(ggplot2)
ggplot2::theme_set(ggplot2::theme_bw())
height <- seq(140, 180, by = 0.01)
density <- dnorm(x = height, mean = 160, sd = 5)
df <- data.frame(
height = height,
density = density
)
ggplot(df) +
geom_point(aes(x = height, y = density),
size = 0.1)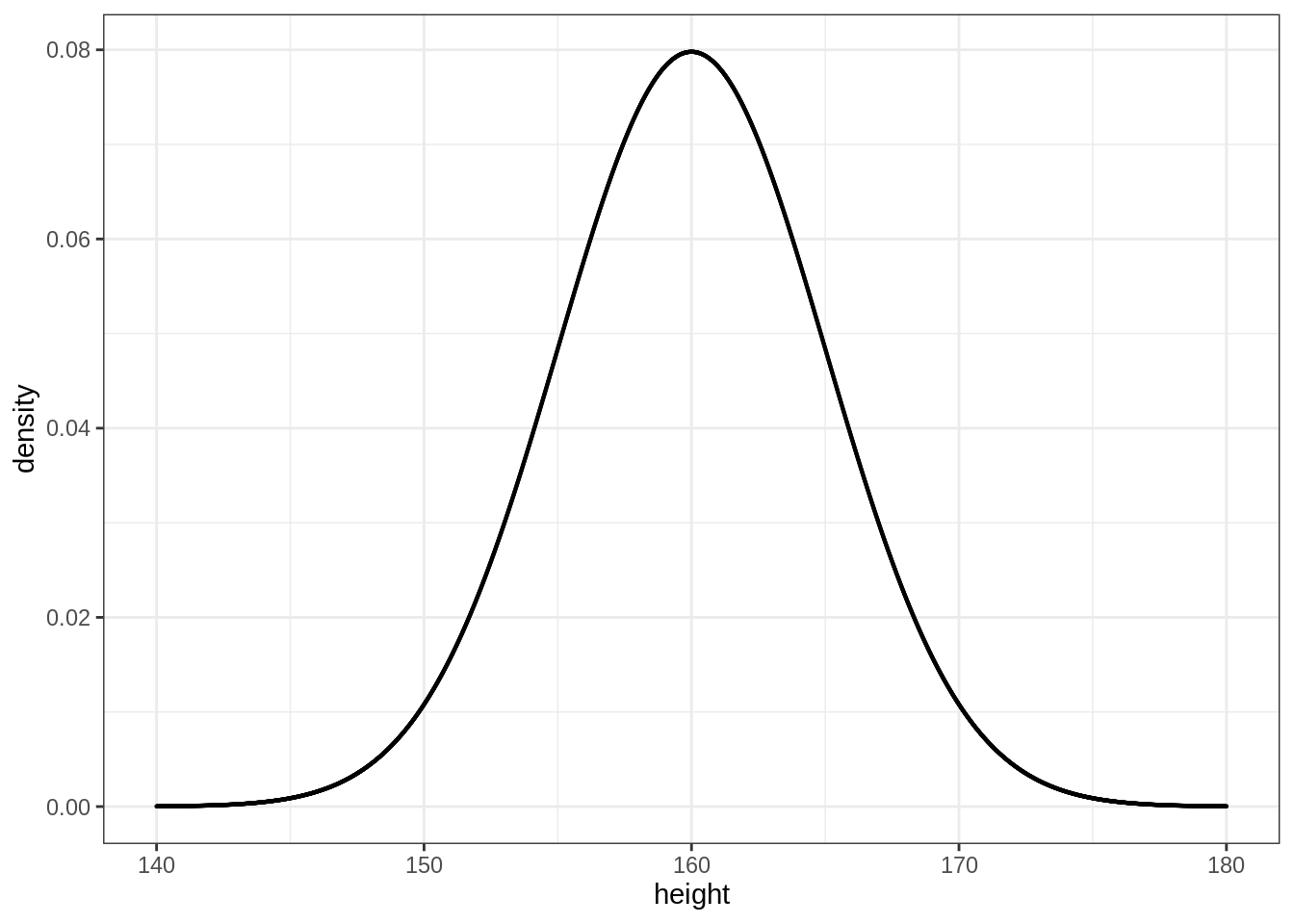
6.1.2 rnorm()
rnorm() 則可以讓我們從常態分配裡取抽取出樣本。例如,若我們想從剛剛的女性身高分配 (\(\mu = 160, \sigma = 5\)) 裡抽取出 3 個樣本:
rnorm(n = 3, mean = 160, sd = 5)#> [1] 153.7023 161.3947 160.6752注意,因為 rnorm() 是隨機抽取14,所以每次的結果都會不同。但當我們抽取的樣本數夠大時,這些樣本形成的分配就會趨近樣本所來自的常態分配。我們可以用 rnorm() 來示範這件事:
sampled_height <- rnorm(n = nrow(df), mean = 160, sd = 5)
mean(sampled_height) # Sample's mean
sd(sampled_height) # Sample's standard deviation#> [1] 159.9382
#> [1] 5.010086我們計算所得到的樣本平均數 (159.938176) 與標準差 (5.0100864) 與原本的常態分配相當接近 (平均 = 160, 標準差 = 5)。
除此之外,我們可以將還可以將原本的分配與抽樣的分配進行比較:
ggplot() +
geom_histogram(mapping = aes(x = sampled_height,
y = ..density..),
binwidth = 0.8, fill = "pink", color = "grey") +
geom_point(data = df,
mapping = aes(x = height, y = density),
size = 0.1)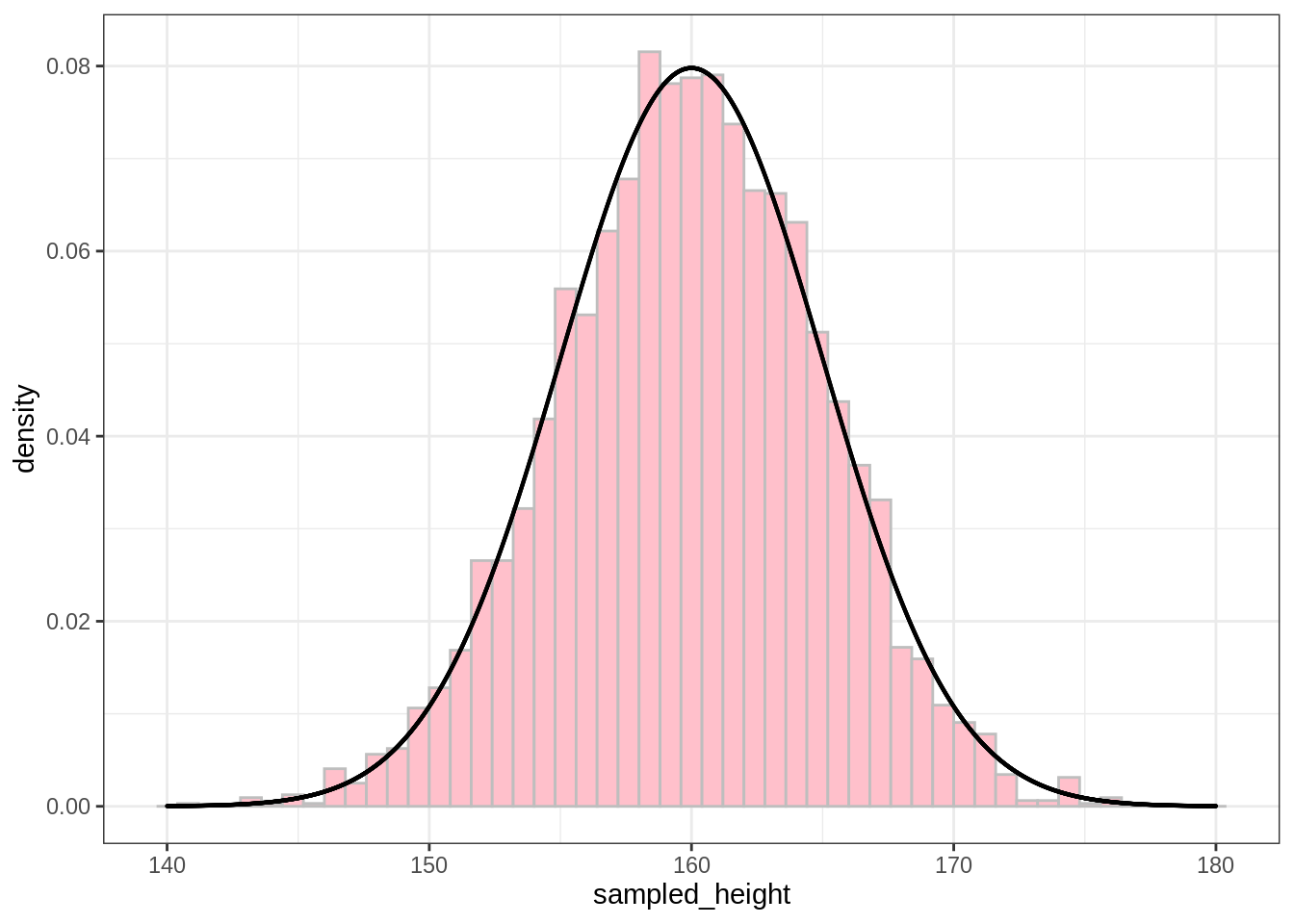
上圖的曲線即是透過剛剛 dnorm() 計算出來的常態分配機率密度。粉紅色的直方圖則是樣本的資料。
6.2 相關 (Correlation)
在 R 裡面,我們可以使用 cor() 計算兩組向量之間的皮爾森相關係數:
# Perfect correlation
x <- 1:60
y <- x + 10
plot(x, y)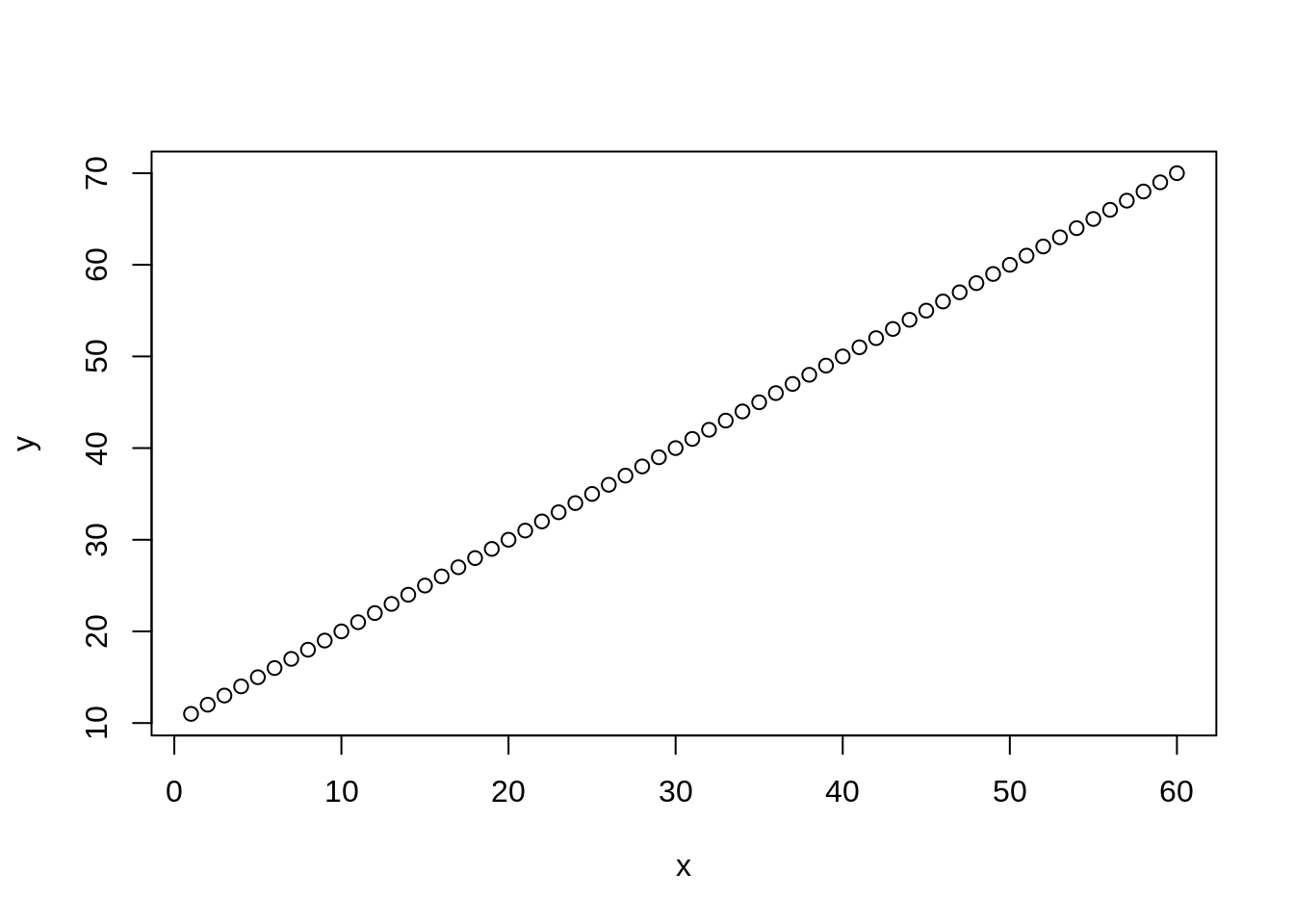
cor(x, y)#> [1] 1我們可以透過 rnorm() 為 y 增添一些雜訊,讓 x, y 的相關不會是完美的:
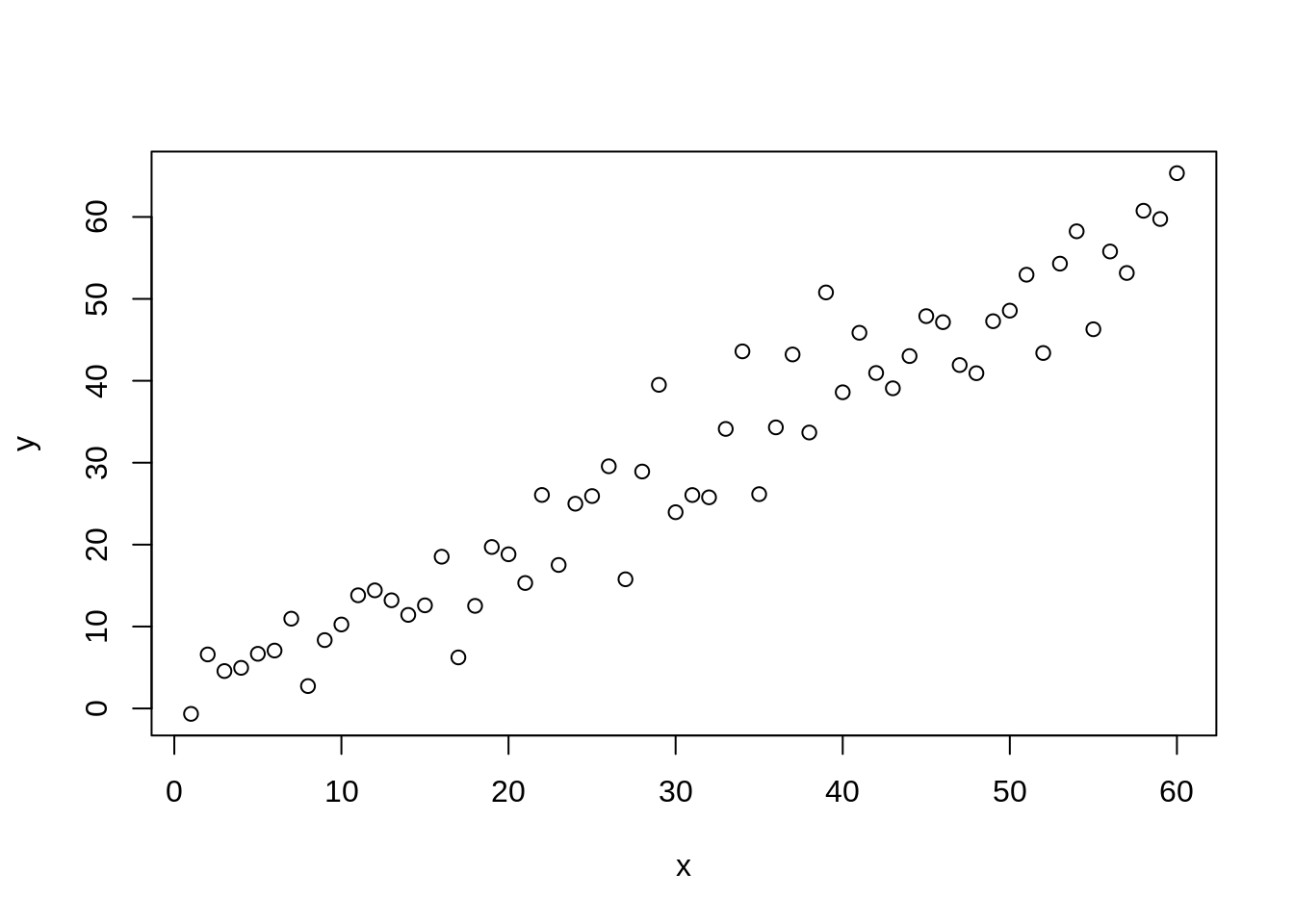
cor(x, y)#> [1] 0.9624822在自然界中,很多變項都呈現常態分配,除此之外,有時候不同變項之間會有線性相關。例如,兒子的身高受父親影響,所以兩者會有正向關係。此外,兩者的身高各自都會呈現常態分配 (有不同的平均與標準差)。透過 rnorm(),我們可以很容易地模擬這些關係:
- 假設父親的身高 \(x_i \sim Normal(\mu=165, \sigma=5)\)
- 假設兒子的身高 (\(y_i\)) 受父親的直接影響:\(y_i \sim Normal(\mu = x_i, \sigma=5)\)
# Simulating correlation b/t two normal distributions
dad <- rnorm(n = 1000, mean = 165, sd = 5)
son <- rnorm(n = 1000, mean = dad, sd = 5)
plot(dad, son)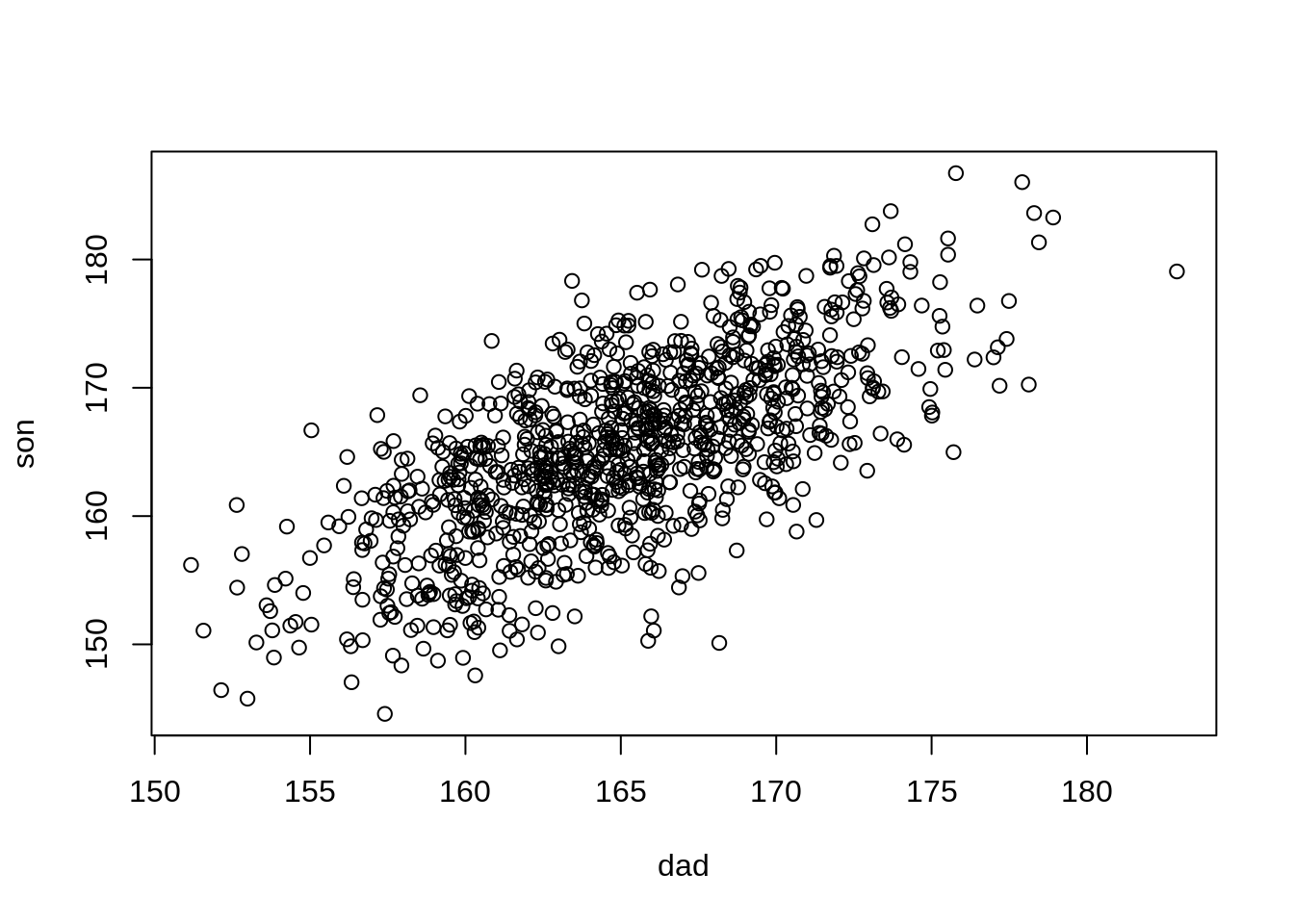
cor(dad, son)#> [1] 0.6906082透過剛剛的模擬,可以得到父親與兒子的身高之間的相關是 0.6906082。學過迴歸統計的同學,應該會記得我們也可以透過簡單線性迴歸得到這個相關係數:若將父親與兒子的身高標準化 (取 Z 分數) 再去做迴歸 \(y = \alpha + \beta x\),則這裡的 \(\beta\) 即會是剛剛所得到的相關係數 0.6906082。
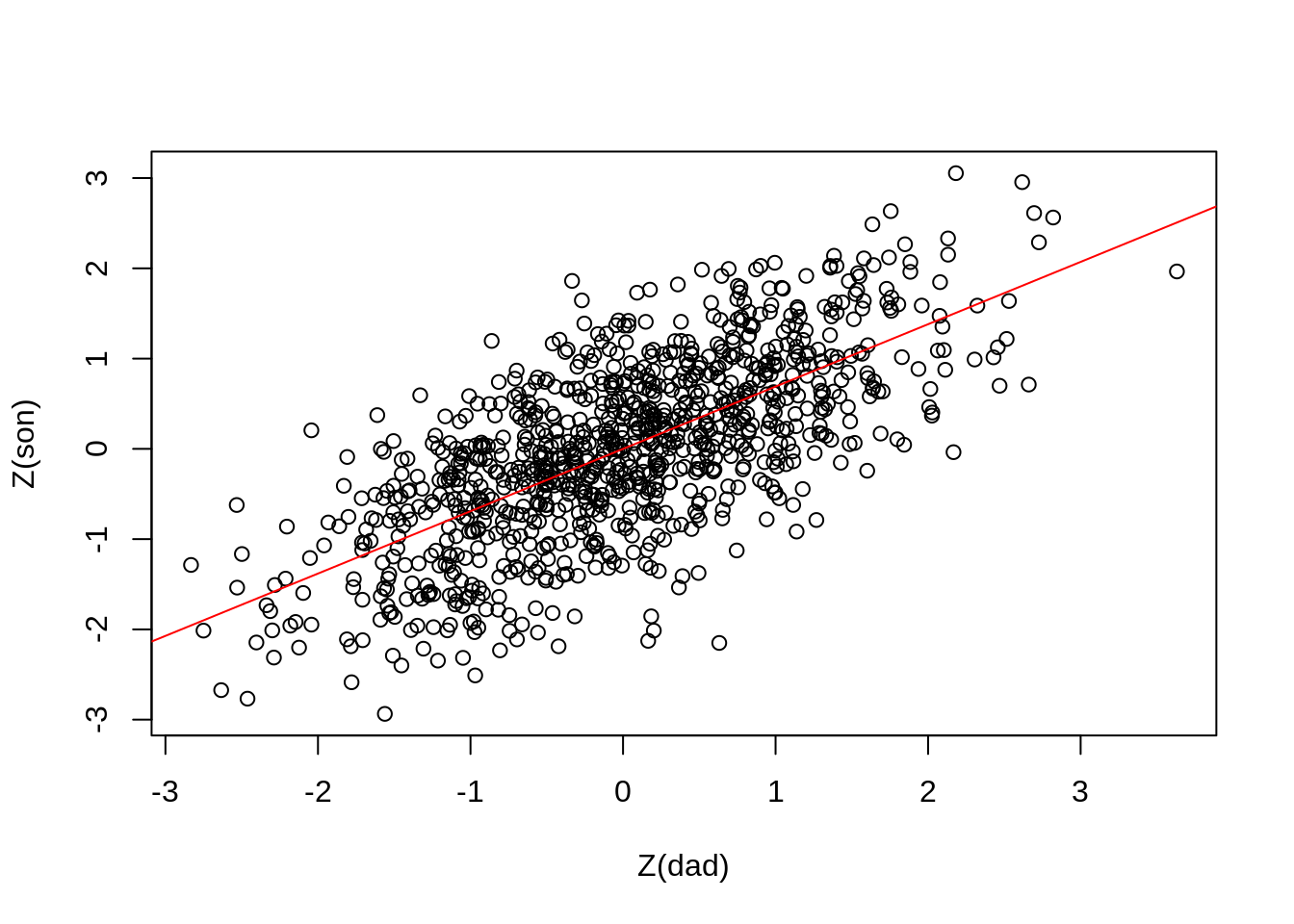
在 R 裡面要使用線性迴歸可以透過 lm()。lm() 裡面放的是公式 (formula),例如下方的 son_std ~ dad_std 即是在表達 \(y = \alpha + \beta x\) 這個關係。
# 標準化
Z <- function(x) (x - mean(x)) / sd(x)
dad_std <- Z(dad)
son_std <- Z(son)
# Simple linear regression
fit <- lm(son_std ~ dad_std)
summary(fit)#>
#> Call:
#> lm(formula = son_std ~ dad_std)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.58588 -0.48222 0.03348 0.51211 2.09151
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.780e-15 2.288e-02 0.00 1
#> dad_std 6.906e-01 2.289e-02 30.17 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.7236 on 998 degrees of freedom
#> Multiple R-squared: 0.4769, Adjusted R-squared: 0.4764
#> F-statistic: 910 on 1 and 998 DF, p-value: < 2.2e-16在上方的輸出裡,Coefficients 的 Estimate 即是 \(\alpha\) (Intercept) 與 \(\beta\) (dad_std) 的估計。可以看到這裡的 \(\beta\) 與先前計算出來的相關係數是相同的。
6.3 因果與相關 (Causation vs. Correlation)
大家應該都知道變項之間相關的存在不代表因果關係的存在15。但當變項間存在因果關係時,(在多數情況下) 變項之間也會存在相關。上方父親與兒子身高的例子,實際上就是在模擬這兩個變項之間的因果關係16。
透過這類模擬,可以幫助我們去理解一些更複雜的概念。接下來,我們要透過剛剛所學的東西去模擬統計學中的混淆因子 (confounder) 與對撞因子 (collider)。
6.4 混淆因子 (Confounder / Confounding Variable)
下方的這張散布圖顯示出一個奇怪的現象:
手搖杯的銷售量越高,溺水的人數就越多
為什麼?難道是因為喝太多手搖杯會讓大家更容易抽筋,進而導致溺水人數的增加?
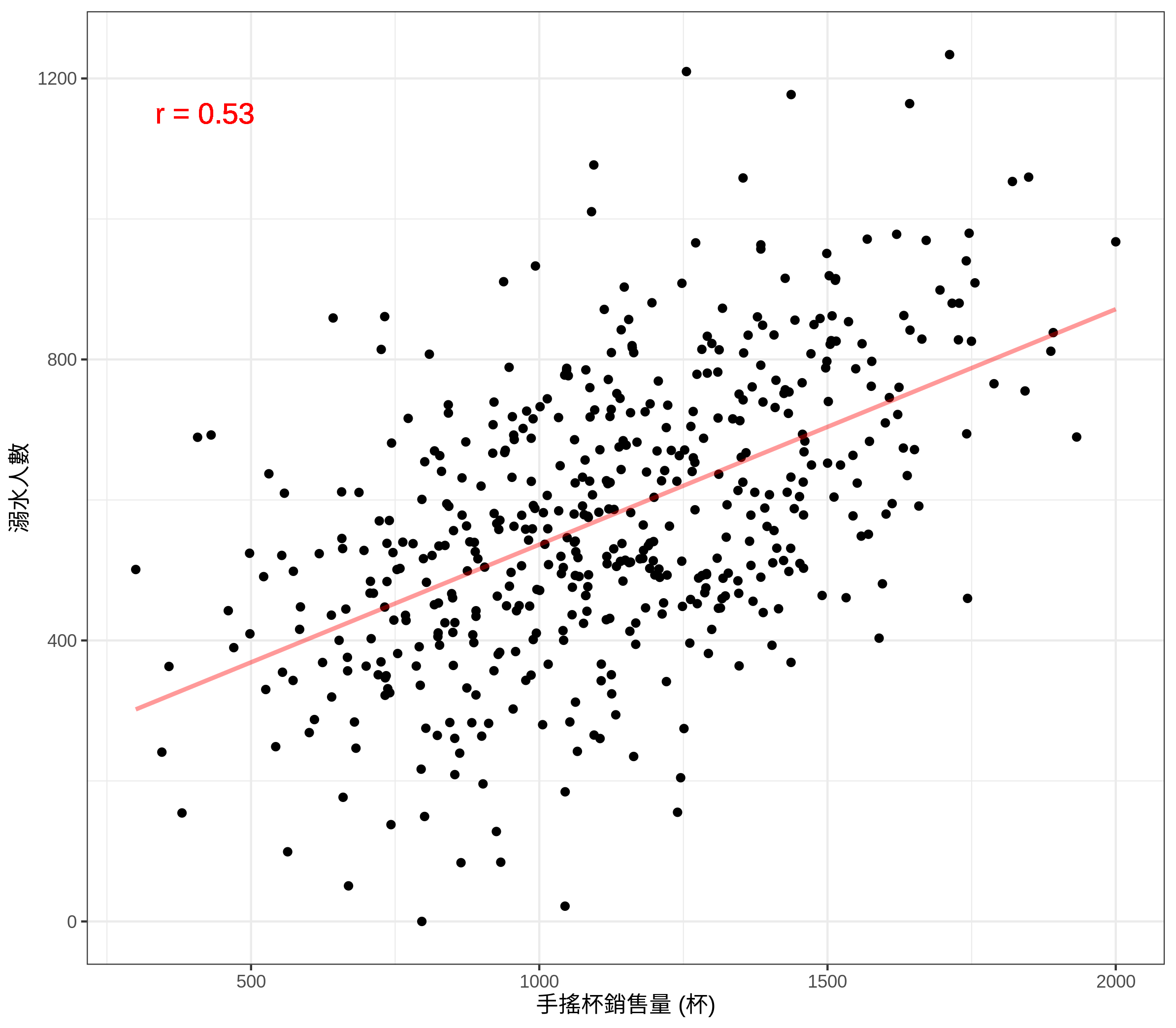
Figure 6.1: 飲料銷售量與溺水人數關聯
這個例子是一個經典的混淆因子的例子。混淆因子 (a.k.a. 混淆變項、干擾因子、干擾變項) 指的是會對多個變項同時施加因果影響的某個變項 (Figure 6.2)。當混淆變項存在時,會造成獨變項與依變項之間產生虛假的關聯,例如:
- 本來獨立的獨變項與依變項,會因為混淆變項而產生關聯
- 本來關聯性不強的獨變項與依變項,會因為混淆變項而變得更強
在上方的例子裡,手搖杯與溺水人數兩者本來應該是獨立的,但因為溫度這個混淆變項使兩者產生了正向關聯:溫度越高,越多人會去買手搖杯 (造成銷售量增高),也越多人會去玩水 (造成溺水人數變多)。
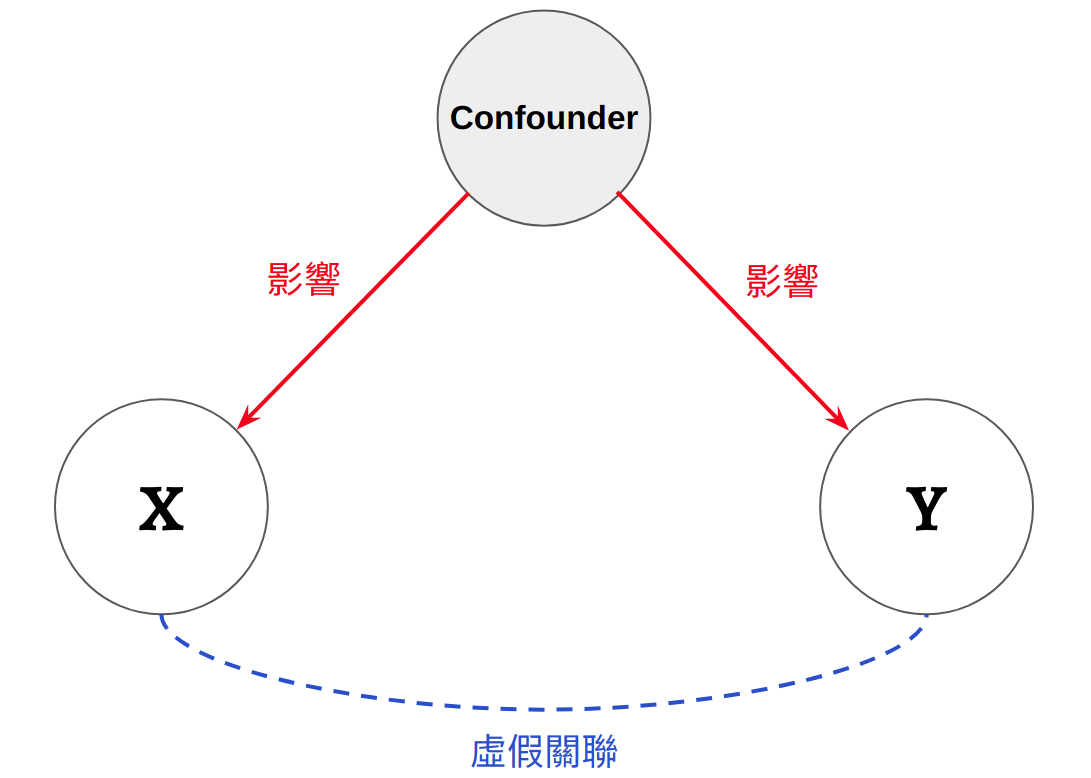
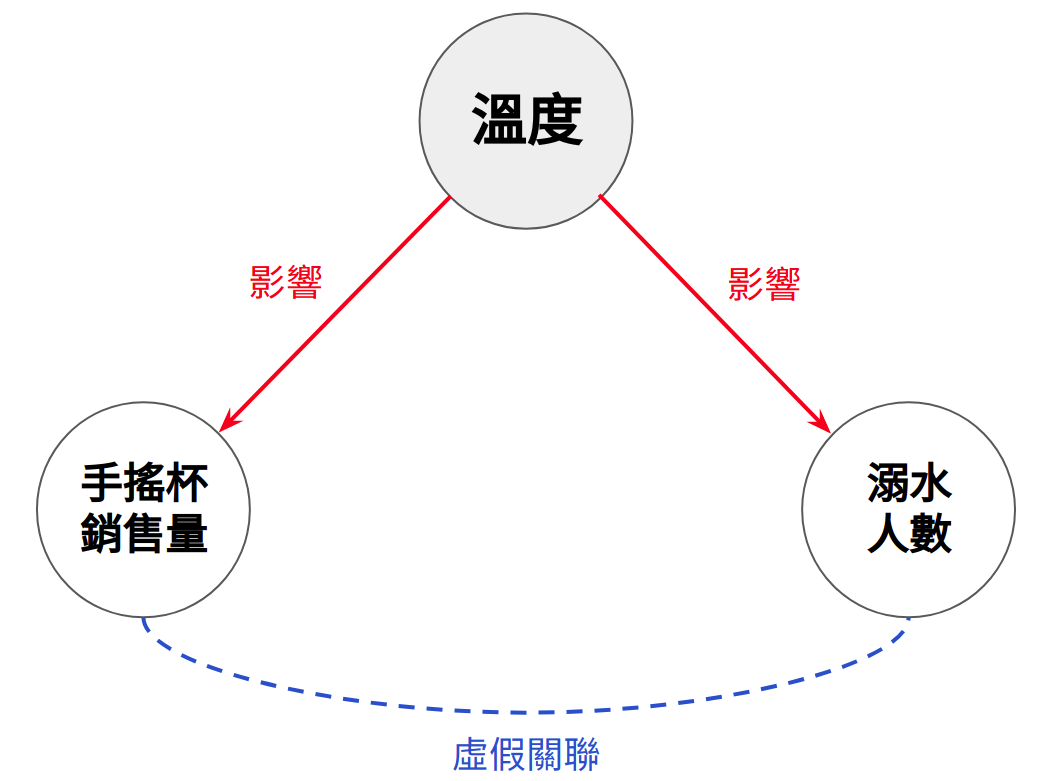
Figure 6.2: 混淆因子 (Confounder)
6.4.1 Simulating Confounder
在 R 裡面,我們可以很容易地去模擬手搖杯的例子。首先,我們先模擬出這三個變項之間的因果結構:
-
temp: 溫度 -
drown: 溺水人數。高溫會造成溺水人數增加。 -
drink: 飲料銷售量。高溫會造成飲料銷售量增加。
set.seed(2021) # Make results reproducible
N <- 500
temp <- rnorm(n = N, mean = 0, sd = 1)
drown <- rnorm(n = N, mean = temp, sd = 1)
drink <- rnorm(n = N, mean = temp, sd = 1)這裡,我們假設這三個變項都來自標準差 = 1 的常態分配。為了讓資料更真實一點,這裡將這些變項做了線性轉換17,讓它們的值落在合理的範圍:
-
temp: 10-40 度 -
drown: 0-1234 人 -
drink: 300-2000 杯
source("functions.R")
# Scale to make data more realistic
df <- data.frame(
temp = minMaxScale(temp, m = 10, M = 40),
drown = minMaxScale(drown, m = 0, M = 1234),
drink = minMaxScale(drink, m = 300, M = 2000)
)接下來,我們就可以看看這三個變項之間彼此的關聯:
# Requires package `psych`, see functions.R
plotPairs(df)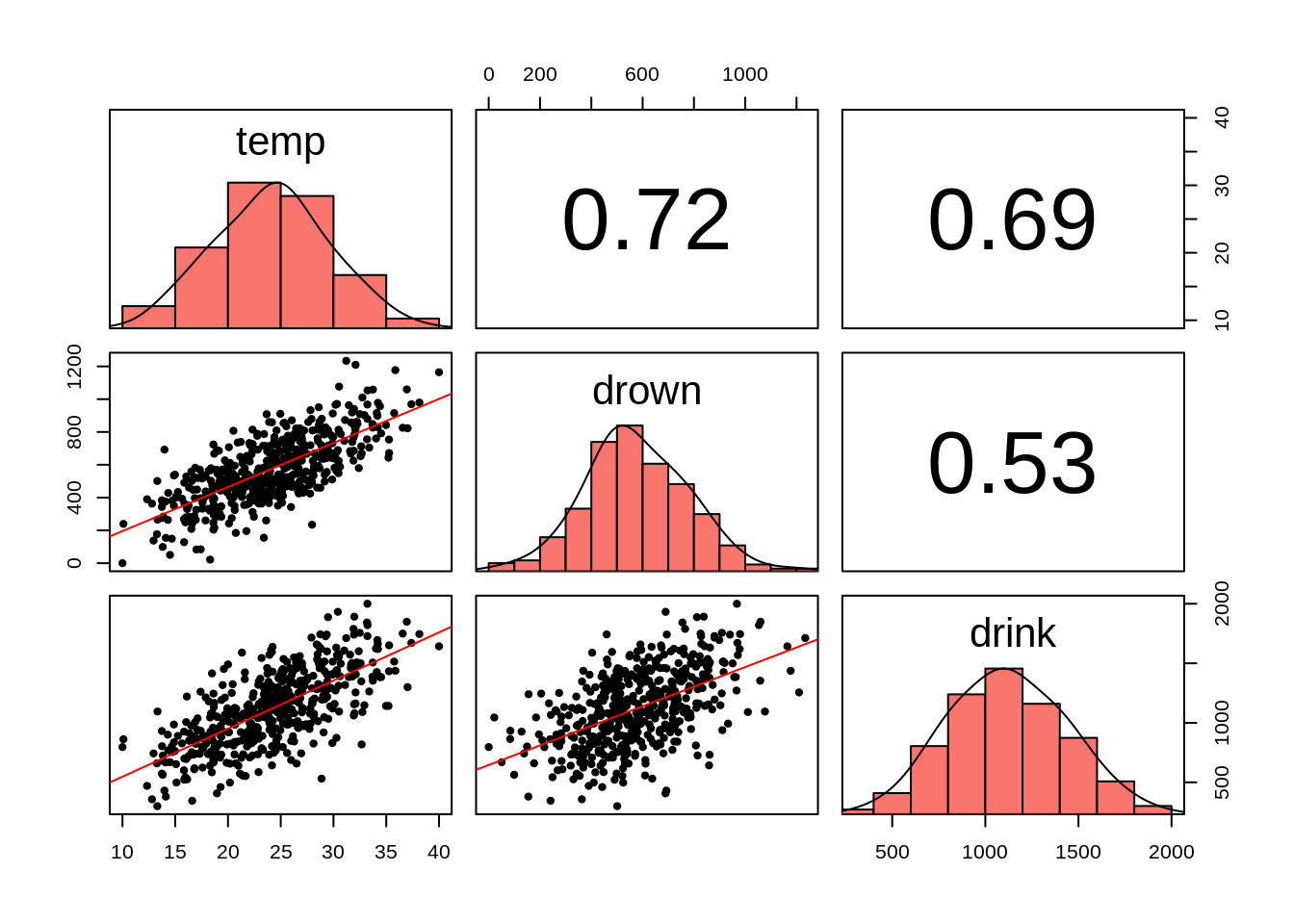
上圖中間那欄最下方 (row = 3, column = 2) 的散布圖即是上方的手搖杯銷售量與溺水人數散布圖 (Figure 6.1)。在 (2, 3) 位置上的數字 (0.53) 即是手搖杯銷售量與溺水人數的相關係數。
6.4.2 Controlling for Confounder
透過這幾張散布圖,我們能夠得知這三個變項之間彼此都有正向關聯。但這些圖本身並無法告訴我們哪些變項造成了哪些變項。要知道這點,我們需要兩個東西:
- 這些變項之間的因果結構 (這樣我們才知道混淆變項是誰)
- 更複雜的統計模型用來控制混淆變項的影響
第一點我們已經知道了 (因為資料是我們自己模擬出來的),但在現實世界中,我們通常不會知道真正的因果結構長什麼樣子。這時候就需要動用領域知識去做出因果結構的假設 (可以有很多種),然後透過資料去檢驗並剔除不符的因果結構。
至於第二點,我們可以使用多元迴歸模型。在只使用簡單迴歸模型的情況下,我們可能會錯誤推斷溺水人數的原因來自手搖杯銷售量:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.896855e-16 0.03809807 4.978874e-15 1.000000e+00
#> Z(drink) 5.250932e-01 0.03813623 1.376888e+01 8.849357e-37但若在迴歸模型中加入混淆變項,模型就會幫我們控制混淆變項的影響。這時,我們就可以得知在沒有混淆變項的影響下,手搖杯銷售量的提升對溺水人數的影響為何:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 6.618100e-17 0.03092700 2.139910e-15 1.000000e+00
#> Z(drink) 4.512621e-02 0.04299789 1.049498e+00 2.944589e-01
#> Z(temp) 6.916087e-01 0.04299789 1.608471e+01 3.604313e-47透過多元迴歸的控制,可以看到 drink 對 drown 的影響從原本的 0.525 變成 0.045。換言之,飲料銷售量對於溺水人數幾乎沒有影響。在簡單迴歸裡,drink 對 drown 的影響其實來自溫度 temp (temp 對 drown 的影響是 0.692)。
6.5 Don’t be a Control Freak
發現了多元迴歸的神奇功能之後,或許會以為在迴歸式裡面加入越多預測變項越好 (我當初就是如此認為),因為這樣就能控制掉任何可能的混淆變項的影響,留下來最「乾淨」的迴歸係數 \(\beta_i\)。這是錯的!!!18不經思考 (沒有因果結構) 地將變項丟進迴歸式裡不但會讓結果難以詮釋,甚至在某些情況下會製造出原本不存在的關聯。
讓我們回到身高的例子。下方這筆資料包含 500 位男性的身高 (son) 以及這些男性的父親 (dad) 與母親 (mom) 的身高:
#> # A tibble: 6 x 3
#> mom dad son
#> <dbl> <dbl> <dbl>
#> 1 158. 178. 173.
#> 2 161. 163. 164.
#> 3 162. 178. 175.
#> 4 151. 163. 157.
#> 5 170. 178. 178.
#> 6 173. 167. 172.假設我們想看父親的身高如何受母親以及兒子的身高影響19,這時我們可能就會很直觀地使用這個迴歸式:
\[ Dad = \alpha + \beta_{Mom} Mom + \beta_{Son} Son \]
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.725574e-16 0.03186325 1.483080e-14 1.000000e+00
#> Z(mom) -5.193205e-01 0.03986636 -1.302654e+01 1.404517e-33
#> Z(son) 8.788082e-01 0.03986636 2.204386e+01 1.282788e-75迴歸式的 \(\beta\) 係數可能會讓我們得到一個結論:
\(\beta_{mom}\) = -0.519,所以…父親越高母親就越矮
所以這代表什麼?矮的女性喜歡跟高的男性結婚?矮的男性也喜歡跟高的女性結婚?要不然為何父親與母親的身高會是負向關係?
6.6 對撞因子 (Collider)
其實在剛剛的資料裡,父親與母親的身高彼此是獨立的。它們之間的關聯之所以會產生,是因為在多元迴歸裡,我們控制了不該控制的變項。這筆身高的資料其實是來自於下圖的因果結構:
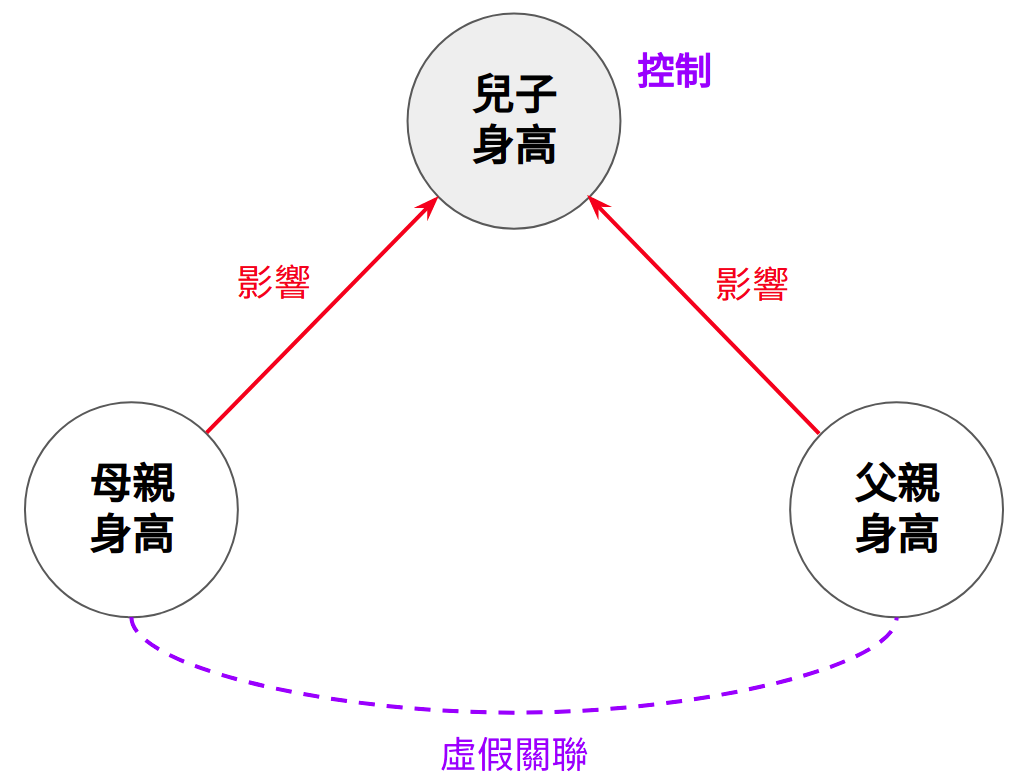
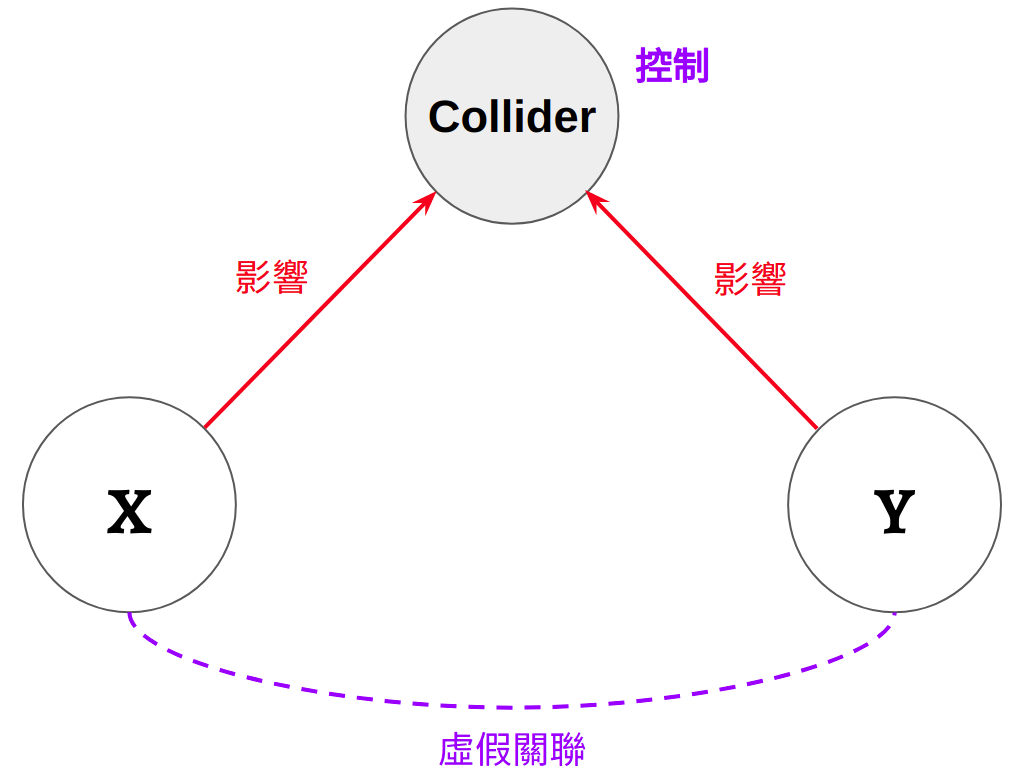
Figure 6.3: 對撞因子 (Collider)
母親與父親的身高對兒子的身高皆有直接的因果影響。在這種情況下,如果我們在迴歸式裡面去控制兒子的身高,就會造成原本獨立的父、母親身高產生虛假關聯。在這種因果結構中,兒子身高的這個變項稱為對撞因子 (Collider)。對撞因子指的是被多個變項直接影響的變項。因為有多個因果影響「匯入」同一個變項,所以稱作對撞因子。
所以為何在控制了對撞因子之後,本來沒有關聯的變項會產生關聯呢?一個直觀的解釋是因為統計上的控制在概念上就是在固定某個變項的數值。所以在固定兒子的身高之後,一旦我知道母親的身高是矮的,我自然就會知道父親的身高是高的;反之亦成立,在固定兒子身高下,若父親是矮的,母親就會是高的20。接下來,我們來看看如何用 R 模擬這個現象。
6.6.1 Simulating Collider
首先,我們透過 rnorm() 模擬出上方的因果結構:
-
mom: 母親身高 -
dad: 父親身高 -
son: 兒子身高。受父母身高的直接影響,且父親與母親的影響程度相同
set.seed(1914) # Make results reproducible
N <- 500 # Sample size
mom <- rnorm(N)
dad <- rnorm(N)
son <- rnorm(N, mom + dad) # dad & mom causally influence son's height
# Scale variables to make them more realistic
df <- data.frame(
mom = 160 + 5 * mom, # Scale to Normal(160, 5)
dad = 170 + 5 * dad, # Scale to Normal(170, 5)
son = 170 + 5 * Z(son) # Scale to Normal(170, 5)
)這裡,我們一樣將各變項進行線性轉換 (非必要),讓資料看起來更直觀一點。我們將母親的身高平均轉換為 160;父親與兒子身高平均轉換為 170;三個變項的標準差皆轉換成 5。現在的這筆資料即與剛剛透過網路讀進來的 collider.csv 內容相同,我們可以透過相同的迴歸模型來檢驗看看:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.725574e-16 0.03186325 1.483080e-14 1.000000e+00
#> Z(mom) -5.193205e-01 0.03986636 -1.302654e+01 1.404517e-33
#> Z(son) 8.788082e-01 0.03986636 2.204386e+01 1.282788e-75現在,若我們將對撞因子 son 從迴歸模型裡剔除,即可看到父親與母親的身高彼此之間沒有關聯:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.587427e-16 0.04476484 -3.546147e-15 1.0000000
#> Z(mom) 7.903449e-03 0.04480967 1.763782e-01 0.8600685透過變項間的兩兩散布圖,我們也可以看到比較合理的趨勢:父母的身高是獨立的,兒子的身高與父母皆為正相關。
plotPairs(df)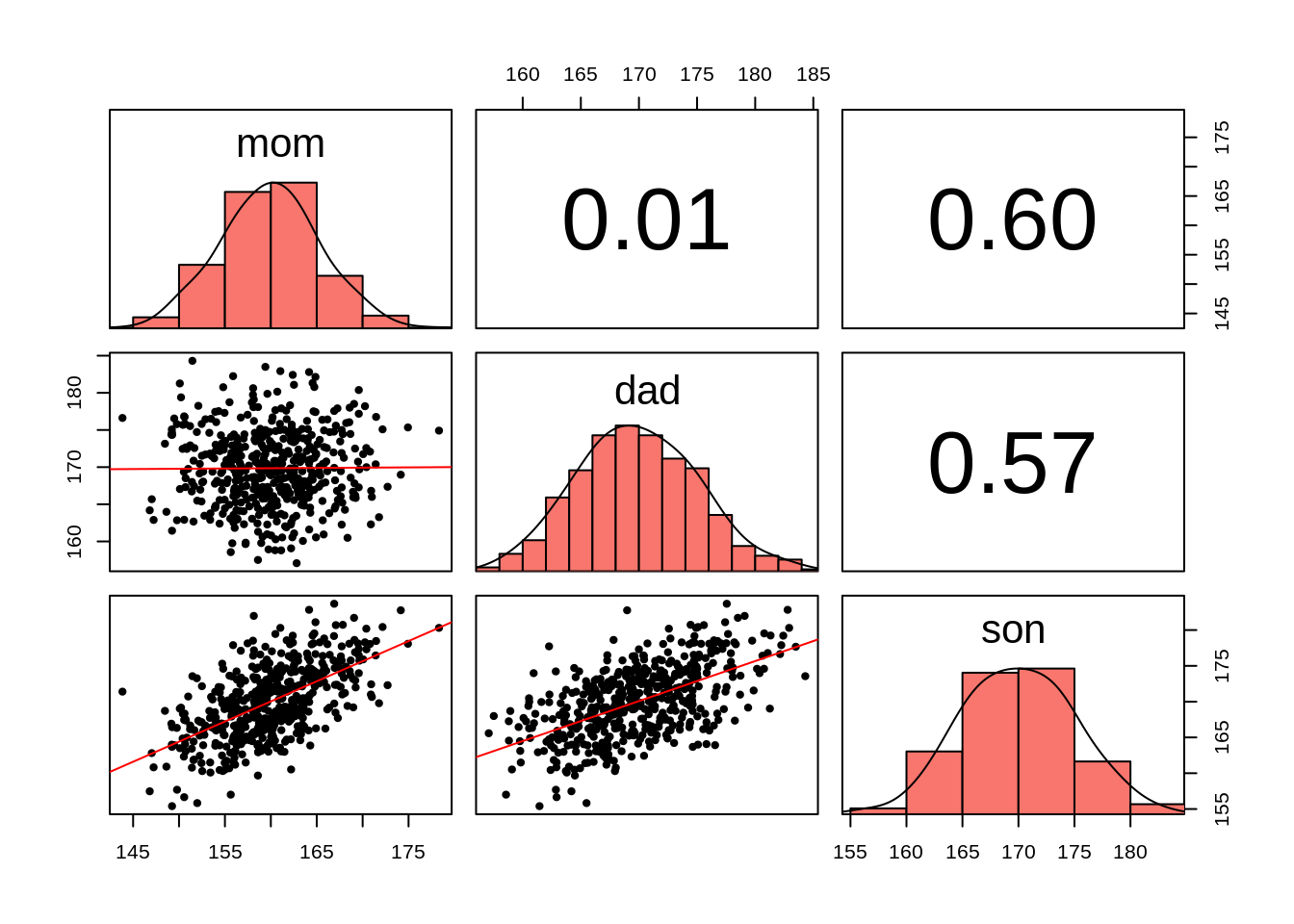
6.6.2 Explaining Collider
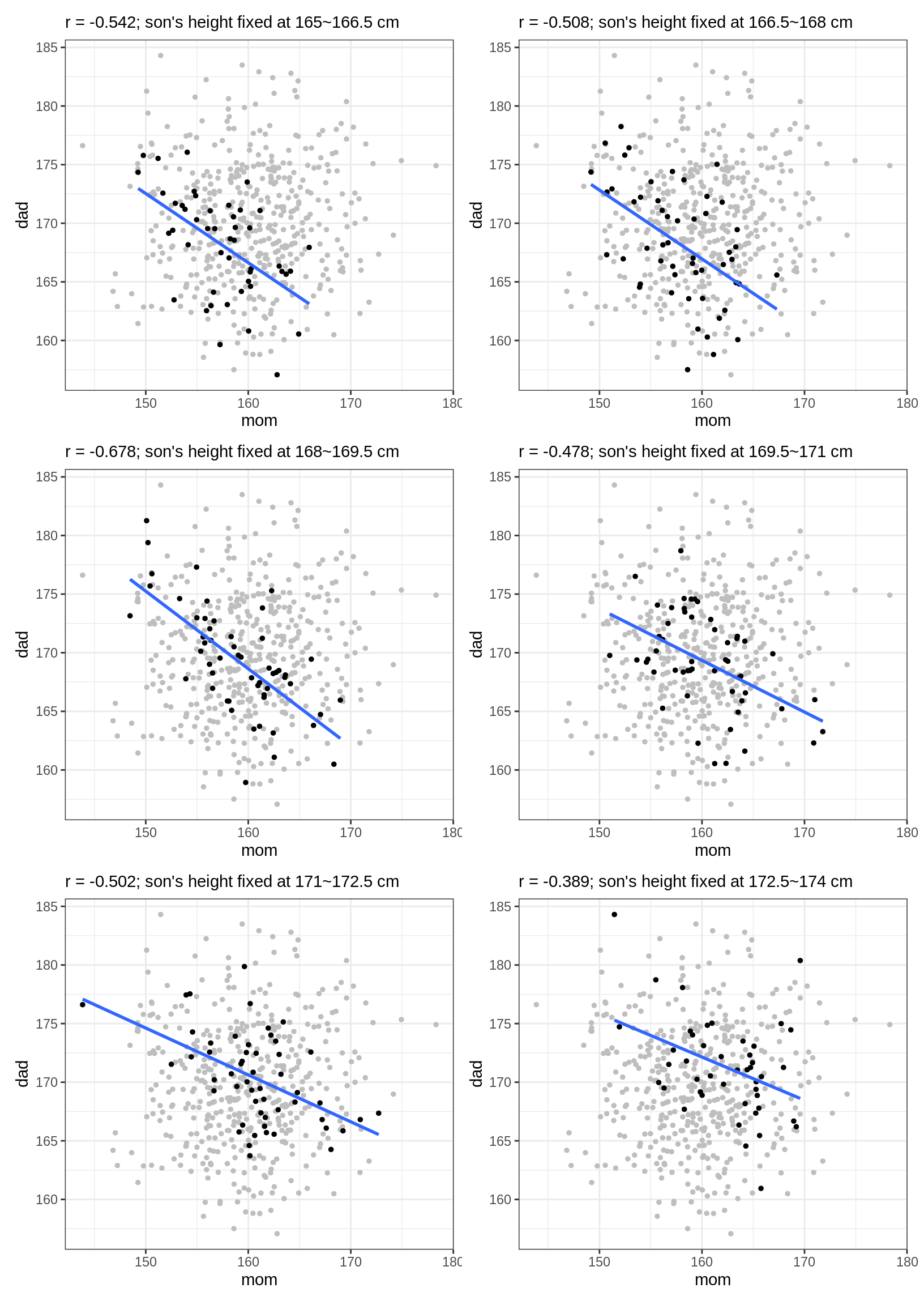
前文只透過文字描述為何「控制」對撞因子會造成原本獨立的變項產生關聯。現在我們可以透過剛剛的身高資料來幫助我們理解這件事情。下方的這幾張散布圖中,灰色的點是所有的資料,黑色的點則是身高被固定在某個數值21的樣本,藍色的線則是透過這些黑色的點所算出來的迴歸線。在這裡我們可以看到控制兒子身高的作用:父親與母親的身高產生了負向相關。
plotRange <- function(df, lower, upper) {
df_filt <- df[lower <= df$son & df$son < upper, ]
r <- round(cor(df_filt$mom, df_filt$dad), 3)
pl <- ggplot(mapping = aes(mom, dad)) +
geom_point(data = df, color = "grey", size = 1) +
geom_point(data = df_filt, size = 1) +
geom_smooth(data = df_filt, size = 1,
method = "lm", se=F) +
labs(subtitle = paste0("r = ", r, "; son's height fixed at ", lower, "~", upper, " cm"))
return(pl)
}
rng <- seq(165, 175, by = 1.5)
plts <- vector("list", length = length(rng) - 1)
for (i in seq_along(rng)) {
if (i == length(rng)) break
plts[[i]] <- plotRange(df, rng[i], rng[i + 1])
}
patchwork::wrap_plots(plts, ncol = 2)